Binary Number Systems

Binary Number Systems#

Lecture#

Note

Whenever you see the Panopto icon or “Lecture” heading, this means there is pre-recorded instructional content as part of this section of a chapter. You’ll need to engage with this content to be able to tackle the application questions.

Panopto logo Binary Number Systems

Key Concepts#

Note

Most times, after you’ve been asked to engage with a recorded lecture, the chapter will include a “Key Concepts” section (like this one!) that highlights key terms and concepts from that lecture. These definitions can help you understand what to focus on or keep track of from the lecture. They also often link out to external sources where you could go to learn more about a particular concept or term. You are not expected to memorize these definitions.

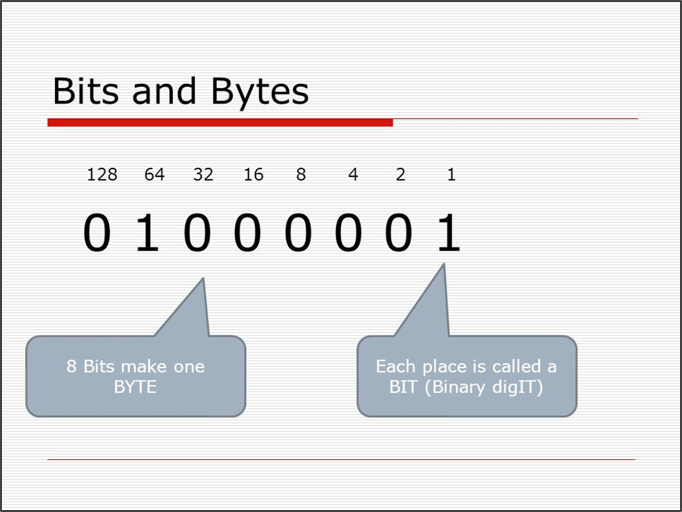
University of Notre Dame main building

Bits

“The bit is a basic unit of information in information theory, computing, including digital communications. As a binary digit, the bit represents a logical state, having only one of two values. It may be physically implemented with a two-state device. These values are most commonly represented as either 0 or 1” (Wikipedia)

Bytes

“The byte is a unit of digital information that most commonly consists of eight bits. Historically, the byte was the number of bits used to encode a single character of text in a computer and for this reason it is the smallest addressable unit of memory in many computer architectures” (Wikipedia)

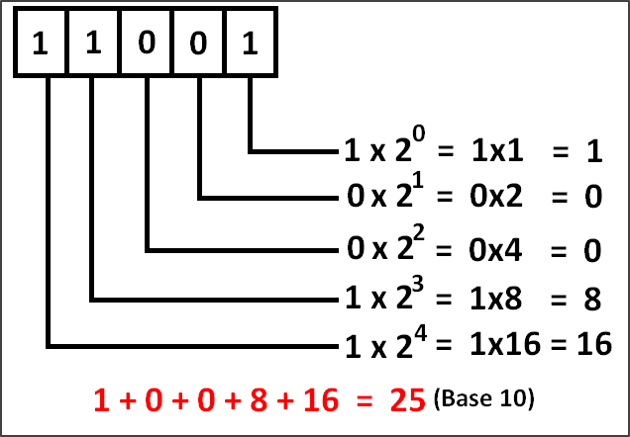
Binary

In mathematics and digital electronics, a binary number is a number expressed in the base-2 numeral system or binary numeral system, which uses only two symbols: typically ‘0’ (zero) and ‘1’ (one). The base-2 numeral system is a positional notation… Each digit is referred to as a bit. Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used by almost all modern computers and computer-based devices” (Wikipedia)

Unit Conversions

  • Kilobyte KB = 1,000 Bytes

  • Megabyte MB = 1 million Bytes

  • Gigabyte GB = 1 billion Bytes

  • Terabyte TB = 1 trillion Bytes

Pattern Ranges

One bit gives us two patterns: 1 and 0. Two bits allow for four patterns: 00, 11, 01, 10. Every time we add one bit to the length of our bitstring, we double the number of available patterns. So, 8 bits or 1 byte provides a means for representing 256 different patterns, as illustrated below:

  • 1 bit – 2 patterns (21)

  • 2 bits – 4 (22)

  • 3 bits – 8 (23)

  • 4 bits – 16 (24)

  • 5 bits – 32 (25)

  • 6 bits – 64 (26)

  • 7 bits – 128 (27)

  • 8 bits – 256 (28)

  • n bits - 2n patterns

Comprehension Check#

Note

Whenever you see the checklist icon or “Comprehension Check” heading, this means there is a set of ungraded comprehension questions that let you test your understanding and get feedback to sharpen your understanding. The application questions will go better if you utilize these comprehension checks.

Clipboard icon Binary Number Systems Comprehension Check

Application#

Note

Each chapter has its own application questions. You’ll see them at the end of particular sections within the chapter. There’s also an “Application Questions” page at the end of each chapter that has all questions from that chapter. Each chapter has a template for its application questions, where you’ll record your answers and responses.

Click here for a Google Doc template with this chapter’s application problems (ND users only)

USB flash drive

Resources:

Q1: What would a byte representing the decimal number 0 look like?

Q2: Calculate the value of byte 01101101.

Q3: How would you representing the decimal number 40 using binary digits?

Contents